The Antenna System Designer
Antenna System Design Engineering
Effective May, 2019:
The Connect802 Antenna System Designer™ On-Line Link-Budget Calculator has been taken off-line.
We apologize for any inconvenience.
In 2010, when the Antenna System Designer was first put on-line, wireless design engineers held the primary responsibility for determining the link budget and suitability of point-to-point microwave links. In todayʻs market, manufacturer engineering support typically stands ready to guarantee the performance of their equipment when their design recommendations as to antenna type, gain, height, and placement are met. Recognizing this, the decision was made to deprecate and remove the Antenna System Designer. If you have specific questions, please Send Us A Message using the button on the top of the page.
Technical Terms Related To Link-Budget Calculation
The following calculator data input and result output fields are listed and described below. Click a term to jump down the page to the explanation and technical notes related to the calculator value.
Frequency - The radio standard or frequency band you're usingDistance Between Towers - Used to determine Free Space Path Loss, attenuation per mile or kilometer, and earth bulgeFree Space Path Loss - The result of the geometric expansion of the spherical RF wavefront as distance increasesTower Height - Used to determine both visual- and radio-Line-of-SightDistance to Obstruction and Obstruction Height - Specifying obstructions between the antenna and the horizonRadio Transmitter Output Power - Used as the starting point for determining the suitability of the linkReceiver Sensitivity - Radio specifications stipulate the bit rates at various received power levelsAntenna Gain - This will normally be a calculated value and is used for link suitability analysisTerrain Roughness - Compensating for the type of terrain underlying the radio-to-radio linkRefractive Index (K) - Adjusting the distance to the horizon for radio waves as opposed to visible lightEarth Bulge - The apparent height of the horizon based on the refractive index (K) of the atmosphereGeodetic Distance - The length of a line from an elevated point to the horizon ignoring any refractive indexVisual / Radio Line of Sight - The apparent distance from an elevated point to the horizon based on the refractive indexRain Fade Margin - Used to adjust link values based on standard rainfall tablesRain Regions and Rain Fade Tables - Tables and graphs used to determine Rain Fade dB in a U.S. regionLink Fade Margin - Additional attenuation to compensate for unanticipated link lossAntenna Maximum Linear Dimension - If provided, this value is used for near-field conflict assessment
Explanations and Technical Notes
The following paragraphs provide technical details of the Antenna System Designer link-budget and antenna height calculator data input and result output fields. If you have any questions, please don't hesitate to contact Maui Communications Networks using the Send Us A Message button on the top of the page.
Value to Enter
Check the button next to either 2.4GHz for 802.11b/g or 5.8Ghz for 802.11a. If you're calculating for a different frequency band, enter the frequency as either Megahertz or Gigahertz and check the appropriate button.
Significance of This Value
Different frequencies experience different degrees of attenuation through obstructions (walls, trees) and in the atmosphere (based on humidity and altitude.) The Connect802 Wireless Network Path Link Budget and Antenna calculator needs to know the frequency band in order to take these factors into consideration.
Background and Technical Perspective
As the frequency of a transmitted signal increases the degree to which the signal strength will be reduced by obstructions increases. An 800 MHz cellular phone signal can pass through several concrete walls and penetrate the interior of some buildings but a 45 GHz point-to-point microwave link has trouble penetrating a strong rainstorm. Consider the fact that frequency and wavelength are related to the speed of light (wavelength=c/F where c=speed of light in m/s and F=frequency in hertz). The following table shows the relationship between wavelength and frequency:
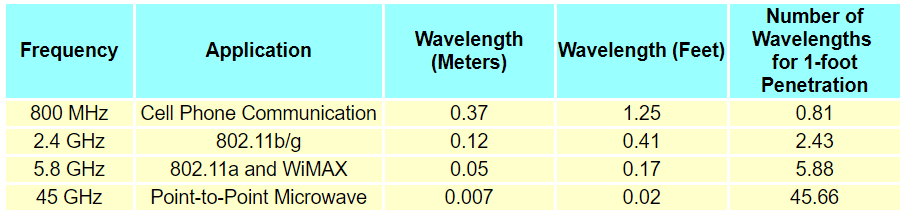
It can be seen from the table above that penetration of a 1-inch obstruction requires more signal cycles at higher frequencies. At higher frequencies the electromagnetic wave is required to interact with an obstruction many more times than at lower frequencies. Consequently, if an 800 MHz signal experienced a 94 dB loss while traversing a particular transmission path the 45 GHz signal would experience a 130 dB loss.
DISTANCE BETWEEN TOWERS
Value to Enter
For outdoor RF, enter the distance between the bases of the antenna towers or mounting points and check the button to indicate whether you're calculating based on Miles, Feet, or Kilometers. The calculator is able to run the Free Space Path Loss equation down to a distance between towers of 1/4" (.04166 feet) with any smaller value being ignored. Plus, for distances greater than 50-feet the calculator will attempt to calculate earth curvature and will process Antenna Height if none is provided.
Significance of This Value
In order to determine the Free Space Path Loss, as well as a number of other calculated values that depend on the distance from the transmitter to the receiver the distance between towers must be entered. Alternatively, if the Antenna Height for both Radio #1 and Radio #2 are entered the Connect802 Wireless Network Path Link Budget and Antenna Calculator will determine the maximum separation distance for the two towers relative to earth curvature and Fresnel zone clearance.
Background and Technical Perspective
NOTE: The calculator allows input of "Distance Between Towers" as small as 1/4" (.04166 feet), an unrealistically small value. When the antennas for which calculations are being performed are too close together the Near Field radiation from one will re-radiate from the other and the actual, measured signal strength will vary significantly from the simple Free Space Path Loss value.
FREE SPACE PATH LOSS: The Expanding Spherical Wavefront and the Inverse Square Law
Jump Back To Top Of Page
As the distance between transmitter and receiver increases the signal strength decreases. As the electromagnetic signal propagates from transmitter to receiver it spreads out in 3-dimensions. Theoretically this expanding wavefront resembles the surface of a sphere. A sphere with radius=2 has a surface are of 50. A sphere with radius=4 has a surface area of 200. When you double the radius the surface area increases by a factor of 4.This gives rise to the "Inverse Square Law" for signal propagation. When distance from a transmitter doubles, signal strength is reduced by a factor of 4. Signal strength varies inversely as a factor of the square of the relative distance. Additional information on antenna radiation can be found on the Wi-Fi: Just the Facts about Antennas page.
Path Loss Modeling and the Real World
The loss of signal strength resulting from transmission through free, unobstructed space, can be estimated with a high degree of accuracy by applying one of several mathematical formulas called "free space propagation models." Modeling formulas have been created to represent a number of different situations including urban areas, areas with many hills and valleys, and generally flat, open areas. These models take into consideration the various effects of signal reflection, diffraction, and refraction, as well as the reduction in signal power resulting from the expanding spherical wavefront.
The Friis Free Space Equation (in decibel form) is commonly presented as the way to determine signal loss through the air between two points. This model calculates signal strength based on the spherical expansion of the propagating wave front. As the "sphere" gets bigger, the surface increases, and, consequently, the density of the propagating signal energy decreases. The Friis equation is the most widely employed formula for calculating path loss and is often seen written in a form similar to the following:
dBLoss = 96.6 + 20 Log10 (distance in miles) + 20 Log10 (frequency in GHz)
You may see this equation presented with a different "constant of proportionality" (the "96.6" value) when the units (miles, GHz) are different. Of course, for a design involving obstructions, building interiors, or specific noise or interference sources, the Connect802 Connect EZ Predictive RF CAD Design, employing RF modeling and simulation software, provides a design that incorporates a more complete picture of the wireless network installation location. Unfortunately, the Friis equation only presents part of the story for practical transmission system design. Many factors, beyond simple spherical expansion, come into play to effect the strength of a transmitted signal.
The relationship between theoretical calculations of path loss and the actual path loss experienced in the real-world has been the subject of many research projects and technical papers. A number of mathematical formulas have been developed to estimate link performance based on the type of link being designed (urban versus suburban areas, smooth versus rough terrain, atmospheric conditions, etc.
There are four widely accepted mathematical models generally used to estimate link attenuation:
- Friis Free Space Path Loss Model
- Loss is based solely on the spherical expansion of the RF wavefront. This model does not consider real-world reflection, diffraction, refraction, and absorption and so always produces results that show a path with significantly less attenuation that will actually be found in practice.
- CCIR Model
- This model, published by the Comite' Consultatif International des Radio-Communication (the CCIR; now the ITU-R), combines Free Space Path Loss with terrain-induced path loss.
- Hata Model
- Based on the CCIR model, the Hata model incorporates empirical measurement curves to represent terrain characteristics for Open, Suburban, Small City, and Large City environments.
- Walfisch-Ikegami Model (WIM)
- The WIM model is tuned for the 800 - 2000 MHz range, and for distances up to 5 km. It takes refraction into consideration for Non-Line-of-Sight connectivity and works well for antenna towers higher than 30 meters.
The results calculated by the actual model formulas differ dramatically. In fact, the Free Space Path Loss model can allow distances between radios that are 200 times greater than what the CCIR model may suggest (these are the two extremes.) A roughly 1 mile these two models may differ by as much as 50 dB, with as much as 70 dB as antenna towers begin to get more then 5 miles apart.
It's not uncommon to hear the common rule-of-thumb that suggests that a 6 dB increase in link budget results in doubling the transmission distance. This rule is correct only for Free Space Path Loss but is unrealistic in the real-world. In fact, the increase in link budget necessary to double the transmission distance varies with the height of the antennas themselves. A low antenna (under 10-feet above the underlying terrain and obstructions) may require as much as 15 dB to double the transmission distance. An antenna that's higher may only need 10 dB (or less.)
The most significant way to improve the performance of a link is to increase the sensitivity of the receiving radio. The receiver's ability to extract a signal from background noise becomes an ultimately limiting factor to link performance. Consider the fact that adding 3 dB gain to a transmitting antenna doubles the transmit signal strength by a factor of 2. This stronger signal then creates stronger signal reflections and is more significantly diffracted than it would have been had the 3 dB gain not been introduced. Hence, 3 dB gain on the transmitter side doesn't translate (in the real-world) into a 3 dB gain by the time the signal gets to the receiver. On the other hand, making a receiver 3 dB more sensitive specifically lets the receiver acquire a signal that is half as powerful as would have been the case if the 3 dB improvement had not been introduced. A 3 dB improvement in receiver sensitivity translates directly (in the real-world) into a 3 dB improvement at the receiver.
The Connect802 Antenna System Designer assumes a modified Hata model and adjusts performance assumptions based on the differences between antenna gain and improved receiver sensitivity. Calculations based on the Hata model formulas suggest that a 10% increase in receiver sensitivity results in a 75% increase in transmission distance.
TOWER HEIGHT
Value to Enter
Enter the height above the ground at which the antenna for Radio #1 and/or Radio #2 is installed. If no heights are entered, or if only one height is entered, and if the Distance Between Towers is provided, the calculator will attempt to determine the unentered values for distance and height. If both antenna heights are entered, but no distance is provided, the calculator will present the greatest distance for the given heights.
Significance of This Value
The tower height is used as input for calculating the distance between towers based on the curvature of the earth. If no tower height is entered then it's assumed that two towers of equal height are used and that they are at the minimum distance apart. If tower height is provided then it's assumed that this is the actual installation height of the antenna, above the ground. Hence, if a value is provided it must take into consideration the required Fresnel Zone clearance and any obstruction height that must be overcome. If only distance between towers is entered then the tower height is calculated based on Radio Line-of-Sight.
Background and Technical Perspective
The following discussion of Earth Curvature and the Visual Line-Of-Sight provides technical perspective on the Tower Height specifications.
EARTH CURVATURE and the VISUAL LINE-OF-SIGHT
Visual line-of-sight extends to the earth's horizon. To calculate the distance to the horizon the assumption is made that the earth's surface is a perfect sphere at which point simple geometry allows calculation. An antenna is some particular height above the ground (the tower height value.) From this height a line is constructed to meet the circle on the horizon and extend to the top of the other tower (a line tangent to the circle that intersects the tops of the two towers). This distance is referred to as the Visual Line-of-Sight (VLOS). Careful study of the geometry reveals that the VLOS distance is very slightly longer than the distance along the ground between two points. The ground distance follows the circumference of the earth and is a measurement of the distance between the bases of the two towers. VLOS is the distance from the top of one tower to the top of the other tower. The towers are perpendicular to the surface of the earth and, hence, tilt "away" from each other slightly (because they are both parallel to radii of the circle). By the Pythagorean Theorem for right triangles it should be evident that the difference between the VLOS and the ground distance is essentially equal to the short leg of the "tilt" triangle (the horizontal, upper-most leg depicted in the diagram to the right.) The distance between the bases of the two towers (along the surface of the earth) can be seen to be slightly shorter than the VLOS distance from tower top to tower top.

The difference between VLOS and ground distance is relatively small in most practical situations. Even a 10-foot (3-meter) tall tower has roughly a 4-mile (6 km) VLOS. That's a difference of much less than 10 feet over 20,000+ feet (3 m over 6 km). Because of this relationship (between tower height and the relatively huge VLOS distances achieved from even a small tower) the ground distance is never considered in field design and measurement. On the other hand, Radio Line-of-Sight differs significantly from VLOS and must be considered.
Jump Back To Top Of Page
The Visual Line-of-Sight
The calculation of Line of Sight begins with an approximation of the Pythagorean theorem for right triangles. Consider the diagram shown below, depicting a right triangle at a point on the spherical earth. Line of Sight distance (d) is a leg of a right triangle. The other leg is the radius (R) of the earth. The length of the hypotenuse is the sum of the earth's radius (R) and the height of the antenna tower above the surface of the earth (ah). It can then be shown that d=sort(R^2-(R+ah)^2). Squaring (R+ah) yields R^2+2Rh+ah^2 and the R^2 term cancels under the root resulting in d=sort(2Rh+ah^2). When considering antenna towers and installation heights, the value ah is generally very small compared with 2R. The 40 feet of height for an antenna tower is very close to being inconsequential compared to the roughly 3952 miles for the earth's radius. As a result, the distance equation can be approximated by removing the +ah^2 term. Removing this changes the solution for the 40-foot tower height from d=7 miles, 2303.2859 feet to d=7 miles, 2300.6459 feet. The approximation changes the result by roughly 3 feet over roughly 7 1/2 miles. Typically the distance-to-the-horizon formula appear in literature only as the 1st approximation. The Connect802 Antenna Designer, too, uses this form.
There is another simplification of the general formula that is common in literature. Often, the constants under the root are solved and a constant of proportionality is created. When the equation is solved with R and ah in miles, the result is in miles. So to if kilometers are used, or feet, or any other unit of measurement. Doing this, however, is not often convenient. One convenient way to represent the formula is with ah represented in feet and d in miles. Hence, under the root, ah is replaced by ah/5280and then the value of ah is in feet, with d being in miles. In this case the value of R is in the numerator under the root, and 5280 is in the denominator. The square root of this fraction is brought out from under the root (and adjusted for the Index of Refraction, discussed below) and you see equations like d=1.22*sort(ah) or some other similar variant based on the conversion between units and the Index of Refraction (discussed below.) In the example, the value 1.22 is the constant of proportionality. Of course, all of these 'simplifications' of the Pythagorean 1st approximation must establish a value to use for R, the radius of the earth.
It is well known that the earth bulges slightly at the equator and is slightly elongated at the poles. The planet is not a geometric sphere but, rather, an ellipsoid. Consequently, a great circle path, covering some predetermined number of degrees of arc, will be longer in some directions than in others. A distance measured on a great circle is called a geodetic line. The United States Department of Defense has adopted a reference system that is considered the best fit for the whole earth. This reference system is called the World Geodetic System, and the most recent base measurements were made a standard in 1984, giving rise to the WGS84 standard.
The WGS1984 ellipsoid uses an equatorial radius of 3963.19 miles and a polar radius of 3940.90 miles. The Antenna Designer uses the average of these two values (3952 miles) as the value for the radius of the earth. This is slightly smaller than the average (based on inhabited land mass) used for GPS navigation (3963 miles) but the difference is, at worst, a more conservative value for the calculation of antenna system design.
Radio Line-of-Sight
Radio signals, like all electromagnetic radiation (such as light), diffract (bend) when they pass from a medium of one density into a medium of a different density. This is how a lens bends light rays (light moves from the low-density air into the higher-density glass of the lens.) This is why a person trying to spear a fish under the surface of the water must adjust their aim (because the fish isn't where it appears to be!)
The earth's atmosphere becomes less dense with altitude. The greatest change in density (per foot of increased height) takes place close to the ground. Consider a radio wave propagating from a vertical antenna. It moves perpendicular to the antenna. Consequently (because the earth "curves away from under the ray") the signal will begin to encounter less dense portions of the atmosphere. This change in density tends to curve the ray back towards the earth. As a result, a signal can, to a small degree, "follow" the curve of the earth around and reach a point that is actually beyond the visible horizon. This distance, which is slightly greater than the VLOS, is called the Radio Line-of-Sight (RLOS). A constant of proportionality of 4/3 is used to relate VLOS to RLOS in standard atmospheric conditions. Standard temperature is 59 degrees Fahrenheit (15 degrees Celsius). Standard barometric pressure is 29.92 inches (1013.25 mb) of barometric pressure. Deviations in temperature and pressure that are consistent with those experienced close to the ground will not effect the practical results of calculations for wireless communication networks. Atmospheric conditions do change dramatically as altitude increases, so interpretation of results for heights greater than 2000 feet should be cautious.
The term "Radio Line-of-Sight" is sometimes used to refer to the radius of the Fresnel Zone. The origin of this usage is unclear and using the term in this way seems to be inappropriate.
DISTANCE TO OBSTRUCTION and OBSTRUCTION HEIGHT
Value to Enter
If a building, tree line, rolling hillside, or other obstruction is present between the installation location for Radio #1 or Radio #2, you may enter the distance to the obstruction and its height to incorporate the obstruction into the Antenna System Designer calculations. Note that the obstruction for Radio #1 must be be between Radio #1 and the horizon, with the same requirement applying to Radio #2. The "horizon" is based on the half-way point when Distance Between Locations is specified. When one installation height, or both heights are specified, the "horizon" is calculated based on the Refractive Index selected.
Significance of This Value
An antenna must be high enough to get above the tallest obstruction between it and the horizon by a factor equal to at least 60% of the first Fresnel Zone radius. The Antenna System Designer calculates all these values. The diagram below depicts the various values used, and calculated, that relate to the distance to the horizon (LOS Distance #1 and LOS Distance #2 in the diagram.) The height of the towers (or other installation locations) determines the respective LOS distance to the horizon. The Refractive Index adjusts the value used as the LOS distance to represent a visual distance, a radio frequency distance, or other distances based on the ratios that all cause a signal to reach further around the sphere of the earth than the flat, geometric calculations would conclude. The values entered into the Antenna System Designer and results returned are represented graphically below.
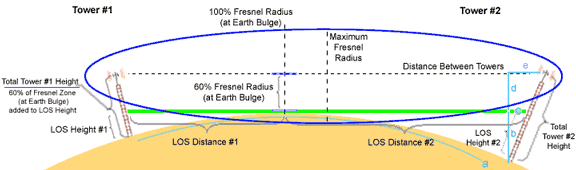
In the diagram above it's interesting to consider the 'tilt' of the antenna tower relative to the distance, annotated on the right-hand side of the diagram as 'a' through 'e'. Distance 'a' is the length, along the ground, between the bases of the two towers. It should be evident that a curved path between two points is longer than the straight line path that could be thought of as the 'Distance Between Towers'. Because the towers 'tilt away from each other' (they're both extensions of radii of the circle) the tops of the towers will be further apart than the bases. In fact, this discrepancy is the distance 'e', the 'tilt' distance. On the one hand, the curved path on the earth is longer than the path from top-to-top, but on the other hand, the tops of the towers tilt away from each other by distance 'e'. The results essentially cancel each other for all practical purposes. Hence, it's assumed that the Distance Between Towers is actually the same as distance 'a', even though, in reality, they are slightly different.
Jump Back To Top Of Page
Here's another aspect to consider. The required height of a tower consists of the height necessary to 'get over the horizon'. This is height 'b' shown above. The tower must be high enough to provide a visual line-of-sight to the horizon. However, the tower must also be high enough to provide 60% Fresnel Zone clearance at the horizon. Height 'd' represents the Fresnel Zone clearance height, with the tower's overall height being b+d. The 'true' height attributable to line-of-sight requirements is actually an extension of the radius of the circle (the 'LOS Height #2' shown in the diagram.) Because the tower 'tilts away' (by a distance equal to 'c') there is a slight error in this part of the calculation as well. As before, this discrepancy is small enough to be ignore for practical calculations. If you're taking the final exam in a math class, however, this type of 'hand waving' won't get you a passing grade!
CABLE LOSS
Jump Back To Top Of Page
Value to Enter
Enter either the total antenna cable loss (for each radio) or the dB loss per foot (or meter) and the length of the cable length. A default value of 3dB is provided for each radio. If you're calculating for Wi-Fi access points with integrated antennas the total cable loss values should be changed to zero for both radios.
Significance of This Value
Cable loss reduces the signal energy between the radio base station and the antenna. A low loss antenna cable (LMR 400) has a loss of 0.23 dB per foot at 2.4 GHz and 0.35 dB per foot at 5.8 GHz. Standard loss cable is often closer to 1 dB per foot. For cable runs less than roughly 10 feet the default value of 3 dB will often suffice for general calculation estimates. When running cable 100 feet up an antenna tower the manufacture's attenuation specifications must be obtained for the cable being used.
Background and Technical Perspective
Electrical resistance is in a cable is the result of opposition to the movement of electrons. The power output of a cable can be derived from Ohm's and Watt's laws when the voltage is not alternating (DC current.) When a signal is alternating (at, for example, 2.4 GHz) the moving electrons tend to push away from the core of the conducting cable and move towards the outside of the cable. This is called the skin effect. In essence, it's as though the cable had less cross-sectional area than the area that is actually present. Skin effect causes the current to occupy a smaller cross-sectional area. Consequently, the relative resistance to current flow is greater for alternating current than for direct current. There are, as might be imagined, a wide variety of manufacturer's options as to cable types, conductor materials, and construction methods to optimize the signal carrying capabilities for a particular frequency, or range of frequencies, and for a particular use.
RADIO TRANSMITTER OUTPUT POWER
Jump Back To Top Of Page
Value to Enter
Enter the transmitter power that will be used for the radio. The value is the power output of the transmitting radio (which is the input power supplied to the antenna distribution system), and not the aggregate output power after considering antenna gain (often called the EIRP, "Effective Isotropic Radiated Power".) A typical Wi-Fi client device (notebook computer, hand-held inventory scanner, PDA, or tablet PC) often has an input power of 30mW. Some high-power mesh routers boast power specifications of 23 dBm (200 mW). For many years a typical 802.11 access point operated at 100 mW (20 dBm).
Significance of This Value
When the two radios are specified with different input power levels, the calculator uses the smaller value for calculations. The single most arbitrarily limiting factor in a wireless network link is the power level of the weakest transmitter. The lowest power level defines performance for both sides of the link. The power level is used by the calculator as part of the link suitability assessment. Power level and antenna gain are attenuated by cable loss, rain fade, link fade, and free space path loss.
Background and Technical Perspective
Radio transmit power is typically configurable within the operating limits of the equipment. There are FCC mandated maximum limits regarding the effective output power when the actual transmit power is focused by some dB gain in the transmission antenna. These are limits on what is referred to as Effective Isotropic Radiated Power (EIRP).
RECEIVER SENSITIVITY
Jump Back To Top Of Page
Value to Enter
Enter the dBm value specified by your point-to-point bridgeradio equipment vendor for the receive sensitivity at a particular desired minimum bit rate for connectivity in the environment. In the absence of vendor specifications you can use the following values for 5 GHz, 802.11n/ac/ax and millimeter wave point-to-point links and be confident that you're reasonably close the a valid receiver sensitivity specification. Remember, however, that your equipment specifications should list actual receiver sensitivity for various data rates.
- For 802.11n/ac/ax operation at the low edge of throughput capability use -85 dBm
- For 802.11n/ac/ax typical operation, use -80 dBm
- For maximum 802.11n/ac/ax throughput and connectivity, use -70 dBm
- For 18 GHz, 23 GHz, 24 GHz, and 45 GHz point-to-point radios and typical operation, use -75 dBm
- For 18 GHz, 23 GHz, 24 GHz, and 45 GHz point-to-point radios and maximum throughput, use -56 dBm
- For 800 MHz cellular use -95 dBm
Significance of This Value
When the calculator makes an assessment regarding the suitability of your collective input values it weighs the power and gain in your system against the aggregate losses (Free Space Path Loss, cable attenuation, rain fade, and link fade.) If the power and gain is able to provide a received signal strength that is at, or above, your specified receiver sensitivity value the link is considered suitable. For perspective, considering that "dBm" is a logarithmic value, an RF signal measured at -56 dBm is 256 times stronger than a signal measured at -80 dBm
Background and Technical Perspective
- Receive Sensitivity
- The signal level required for proper operation of a receiver is called its receive sensitivity. In order to get signal to the receive circuitry at a level above the noise floor it's necessary to overcome several additional losses in the receiving radio unit. Antenna coupling loss is an example of what must be overcome to achieve a circuit signal level above the noise floor. The antenna element has energy induced into it by the fluctuating electromagnetic field coming from the transmitter. This energy must be transferred to the wires, circuit board traces, IC's, and discrete components making up the receiver circuitry. The energy transfer occurs through an antenna coupling. Often this takes the form of a pair of inter-circled wire loops in the form of an electrical transformer (called inductive coupling. Antenna coupling introduces loss.
- Noise Floor
- The circuitry in a radio receiver must be capable of electrically manipulating the current induced into the antenna by the radio signal. The induced signal is very weak. Radio circuitry is electronic in nature and therefore creates some amount of heat when electricity flows through it. This heat causes electronic noise in the receiver circuitry. An expensive piece of equipment is designed to produce less internal thermal noise. As might be imagined, signal energy can not be distinguished from thermal noise when the signal energy if very weak. This level is called the noise floor for a receiver.
ANTENNA GAIN
Jump Back To Top Of Page
Value to Enter
Enter the dBi gain value for the both antennas. Even a standard antenna has some gain, that's just the nature of the underlying physics. Many 802.11 access points come with an antenna roughly 3- to 5-inches long as standard equipment. This type of antenna has a gain of 2.15 dB, which is the default value for the calculator.
Significance of This Value
The antenna gain is used by the calculator as part of the link suitability assessment. Power level and antenna gain are attenuated by cable loss, rain fade, link fade, and free space path loss.
Background and Technical Perspective
A theoretical point source that radiates an electromagnetic field does so in a perfect sphere, with energy propagating outwards equally in all directions. This theoretical antenna is called an isotropic radiator. The simplest real-world antenna is a length of wire, called a dipole radiator. Signal energy from a dipole radiates outward to the sides (perpendicular to the length of the antenna) but not out the ends. This is analogous to the way light shines out of a fluorescent light tube. The transmission volume has a torus shape (doughnut shape) around the radiating element. Instead of radiating out in a spherical shape the energy is "flattened" into a torus. Relative to a sphere, the torus has less volume for the same radius. The density of energy in the torus is greater than that of the sphere (in the direction perpendicular to the antenna.) This is a basic antenna gain factor that is the natural result of the way a dipole radiator creates the electromagnetic field.
Gain measured relative to a theoretical isotropic radiator is assigned the measurement unit "dBi" (decibels relative to isotropic.) Unless specified otherwise, if you see a gain expressed simply as "dB" it probably implies "dBi". The inherent gain of a dipole antenna is 2.15 dBi. The dipole, by the nature of the toroidal field volume, introduces this gain. An alternative unit of measurement is to specify gain in terms of "dBd" (decibels relative to a standard dipole). Although less common, dBd is sometimes given in antenna specifications. An antenna with 0 dBd gain has a gain of 2.15 dBi.
REFRACTIVE INDEX
Value to Enter
K=4/3 is the most common value to use to represent the RF refraction (degree of bending) in the earth's atmosphere
Surveyors often use K=6/3 and this results in what is commonly called the "Visual Line-of-Sight"
For elevations greater than 5000 over Mean Sea Level use the Low Density, K=2/3 value (i.e.: Denver, Colorado)
Use K=Infinity for "flat earth" calculations. These are slant-range designs where one antenna essentially looks "up" at the other, whether it's up to the top of a very tall building or from an earth station to a satellite.
Use K=1 to solve distance-to-the-horizon calculations as if the earth were a perfect, geometric sphere, with no refraction effects considered.
Significance of This Value
The Refractive Index or "K" value is used by RF designers, radio operators, astronomers, surveyors, and others to adjust measurements to compensate for the "bending" (refracting) of signals as they pass through the atmosphere. The value K=4/3 is the most commonly used but will result in the most optimistic measurements. It means that a signal can travel 4/3 further than the physical horizon. A value of K=1 is unrealistically small and results in the measurements being made as if the earth were a geometric sphere. Surveyors often use 6/5 as a reasonable estimate of atmospheric refraction but, at the highest elevations (over 5000 feet MSL) values as low as K=2/3 are used.
Background and Technical Perspective
When performing computations or analyzing data related to spatial relationships it's necessary to understand the differences in measurements for distances on the earth's surface. Data obtained from, or applied to, the real earth (surrounded by a real atmosphere) typically differs from that which would be obtained based on the assumption of a spherical earth and derived using Euclidean or planar metrics. The geometric calculations that could be performed are based on distances being assumed to be a length of an arc of a great circle on a sphere. This geometric result is called a geodetic line, and it is the distance between two points (an antenna and the horizon, for example) that would be experienced by a person walking along a road between the two points. On the other hand, the changes in atmospheric density caused by altitude (density decreases as altitude increases), temperature (hot air is less dense than colder air), and water vapor (moist air is less dense than dry air.. a fact that may seem 'backwards' but it's true.)
When an wave moves from a region of lesser density into an area of greater density it bends towards the denser medium in accordance with several well established principles of physics. The pencil in the glass of water (below) appears to bend as it enters the water because the water is denser than air. The degree to which a propagating wave bends is represented by the refractive index for the medium through which the wave is passing. The refractive index is often represented by the capital letter "K".

THE GEODETIC DISTANCE
Consider the effect of signal refraction on a propagating radio signal, as depicted in the diagram below. If there were no refraction then the signal would simply travel in a straight line and strike the earth at the horizon. This path is called the geodetic line. The geodetic can never be observed in the real world. The distance to the horizon based on zero refraction (K=1) could be geometrically calculated considering the earth to be a sphere. The lines tangent to the geometric sphere, taken in conjunction with the radius, would allow calculation of the true geodetic distance to the horizon from an antenna.
In practice, however, the refractive index of dry air is roughly 6/5 (K=6/5) and a surveyor, using an optical instrument (a "transit") to determine the distance between two points, must reduce the observed measurement by this factor. Assuming the K=6/5 yields the Visual Line-of-Sight distance to the horizon. This is, "how far can I see?"
The most typical refractive index for RF design is K=4/3. This is the refractive index of water and there is water vapor (to varying degrees) in the atmosphere. Of course, refraction is the result of the varying density in the atmosphere. The air closer to the ground is (generally) more dense than that at higher elevations. The result of this variance in density is that the distance traveled by an RF signal (the Refracted Ray, shown above and to the right) is greater than the geodetic line (the "Visual Line-of-Sight". RF can "see" slightly beyond the visible horizon.
How far can it "see"? If you were at an elevation such that the geodetic line to the horizon were exactly 10 miles then (using the refractive index of dry air, K=6/5) you would see the horizon 12 miles away (6/5*10=12). Using K=4/3 (typical for RF design) the "Radio Line-of-Sight" (also called the "Radar Line-of-Sight") would be 13.3 miles away (4/3*10=13.33).
Occasionally a reference is made to "K=Infinity". This is referred to as the "flat earth" scenario where there is no geodetic line; a wave continues to propagate forever without striking the earth's horizon. This is the scenario that exists when considering the communication path from an earth-based radio to an orbiting radio. The propagation that's of interest is "up" and not "horizontal". Hence, by setting K=Infinity calculations can be performed on "slant range" links. This is also the case when the roof-mounted antenna on a 20-story building is transmitting down to the roof of the 2-story building a few miles away. The Connect802 Antenna Designer takes these factors into consideration.
EARTH BULGE
Jump Back To Top Of Page
This value is calculated based on the distances involved
Significance of This Value
The term "earth bulge" and "earth height" are often used interchangeable. It's generally considered that the term "earth bulge" refers not to the actual height of the ground (relative to the center of the earth) but, rather, to the apparent height that creates an obstruction for an electromagnetic wave. This apparent height is calculated based on the refractive index of the atmosphere. It's only when K=1 that the apparent height of the earth bulge is equal to the actual height of the earth at a particular distance.
Background and Technical Perspective
Refer to the Refractive Index discussion (above) to understand how the curvature of the earth appears greater than the physical, geometric spherical representation that might be used to calculate line-of-sight to the horizon based on a tangent line from a point at some height above the surface.
RAIN FADE MARGIN
Value to Enter
Enter the dB loss per mile, or per kilometer, associated with Rain Fade for the entire end-to-end link. This value can be derived from the standard tables shown (and explained) below or from actual field measurements. If you're unsure, and if you live in an area where rainfall can be heavy and prolonged, use 0.8 dB/mile (0.5 dB/km) as a 'worst-case' value for Wi-Fi, WiMAX or other system operating below 10 GHz. Between 57 GHz and 64 GHz you should enter a value of 12 dB/km to account for oxygen absorption.
Significance of This Value
For frequency management and general planning purposes it may be sufficient to make simple (and optimistic) assumptions based on Free Space Path Loss (which accounts for spatial spreading losses.) Additional detail can be incorporated into a design model to improve the accuracy of the predictions. The International Telephony Union (ITU) has a number of recommendations described in the ITU Radio Regulations (ITU-R P.620-5, ITU-R P.837-4, ITU-R P.1546-1, and revisions in ITU-R P.620-5). Weather monitoring stations around the world report rainfall rates which are used to determine both average rain amounts as well as local gradients in rainfall (where, for example, a low-lying area receives more or less rainfall than a higher-elevation location a few miles away.)
The degree to which signals are degraded in the atmosphere is dependent on two factors:
- The disruption of transmitted RF signal energy by water droplets and vapor
- Water vapor is resonant between roughly 22 GHz and 183 GHz and it's between these frequencies the worst-case rain fading occurs
- The transfer of energy to oxygen molecules in the atmosphere (referred to as "oxygen resonance")
- This factor is not related to rain fade and is presented here only for perspective.
- The natural vibration of water molecules becomes resonant at two specific frequencies: 60 GHz and 120 GHz. At these two frequencies, transmitted RF energy strength is diminished due to energy transfer to oxygen molecules. In the present set of considerations, this only applies to 60 GHz, unlicensed point-to-point links and accounts for the fact that they are usable only up to a maximum distance of just over 2000 feet.
For in th 2.4 GHz spectrum you may find attenuation up to 0.08 dB/mile (0.05dB/km) in the heaviest of rain conditions (4 inches/hr). A thick fog may result in as much as 0.03 dB/mile (0.02 dB/km) attenuation. In the 5 GHz spectrum the attenuation may be up to 0.8 dB/mile (0.5 dB/km) in heavy rain and 0.11 dB/mile (0.07 dB/km) in fog. Even a light rainfall or heavy dew that collects as droplets on tree leaves can introduce as attenuation that's similar to a heavy continuous rainfall. The 60 GHz frequency is significantly impacted more by a physical property of oxygen atoms called "oxygen resonance" than by rain and this limits 60 GHz links to roughly 1/2-mile or less.
Background and Technical Perspective
As the transmitted signal energy passes through water droplets it is both absorbed and scattered to varying degrees. Absorption is the aspect where part (or all) of the energy is converted to heat as it penetrates the water droplet. Scattering is the disruption of the direction of travel of the RF signal as it passes through the non-uniform shape, and differing density of the water droplet. Scattering may cause refraction of the wave (bending due to the difference in density between the air and the water) or diffraction (bending of the signal around the edges of an object that is smaller than 1 wavelength.) Some perspective is:
- Above 18 GHz, rain causes roughly twice the impact in terms of link outage as compared with lower frequencies
- The longer a link is, the greater the probability of a point-to-point link being disrupted by rain
- On the plus side, millimeter wave links experience less multipath fading in the rain so the fade margin is decreased
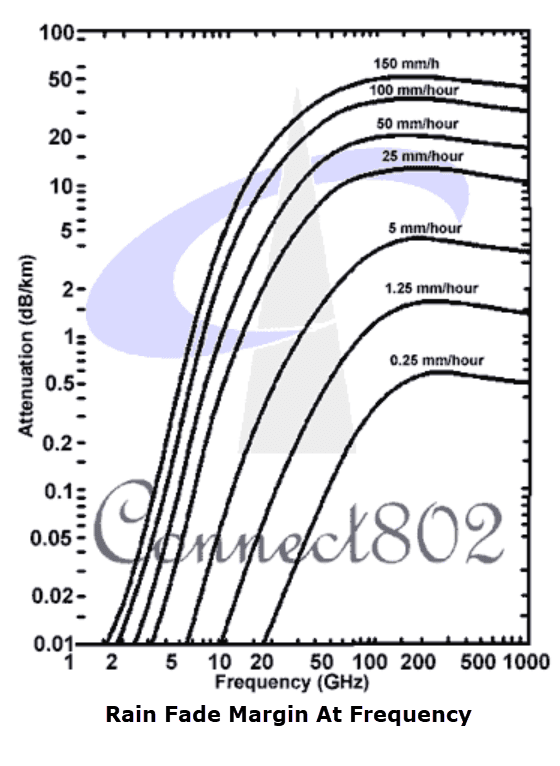
In the United States, use the Rain Fade Region Map with an accompanying Average Rainfall Table to get an idea of the rainfall rates then refer to the Rain Fade Margin Graph for specific attenuation values at various frequencies.
Rain Regions in the United States
To use the Rain Fade tables:
- Determine your Rain Region from the map below. Note that for the State of Hawaii, there are numerous local changes in rain fade over short local distances. Hawaii can be considered Region E in the rain-prone areas.
- Note the number of Hours Per Year the rain rate occurs and the Rain Rate (mm/hour)
- On the second graph below (Rain Fade Margin At Frequency), locate the Rain Rate curve (mm/hour) corresponding to your Rain Rate, find your frequency of operation on the horizontal axis, and read the expected Rain Fade (dB) on the vertical axis.
- On the third graph below (Background Atmospheric Attenuation), determine the amount of attenuation (dB) that's always introduced by the combination of normal moisture and including oxygen resonance attenuation.
- Add the Rain Fade dB value and the Atmospheric Attenuation dB value. That's your total Rain Fade Margin for your link.
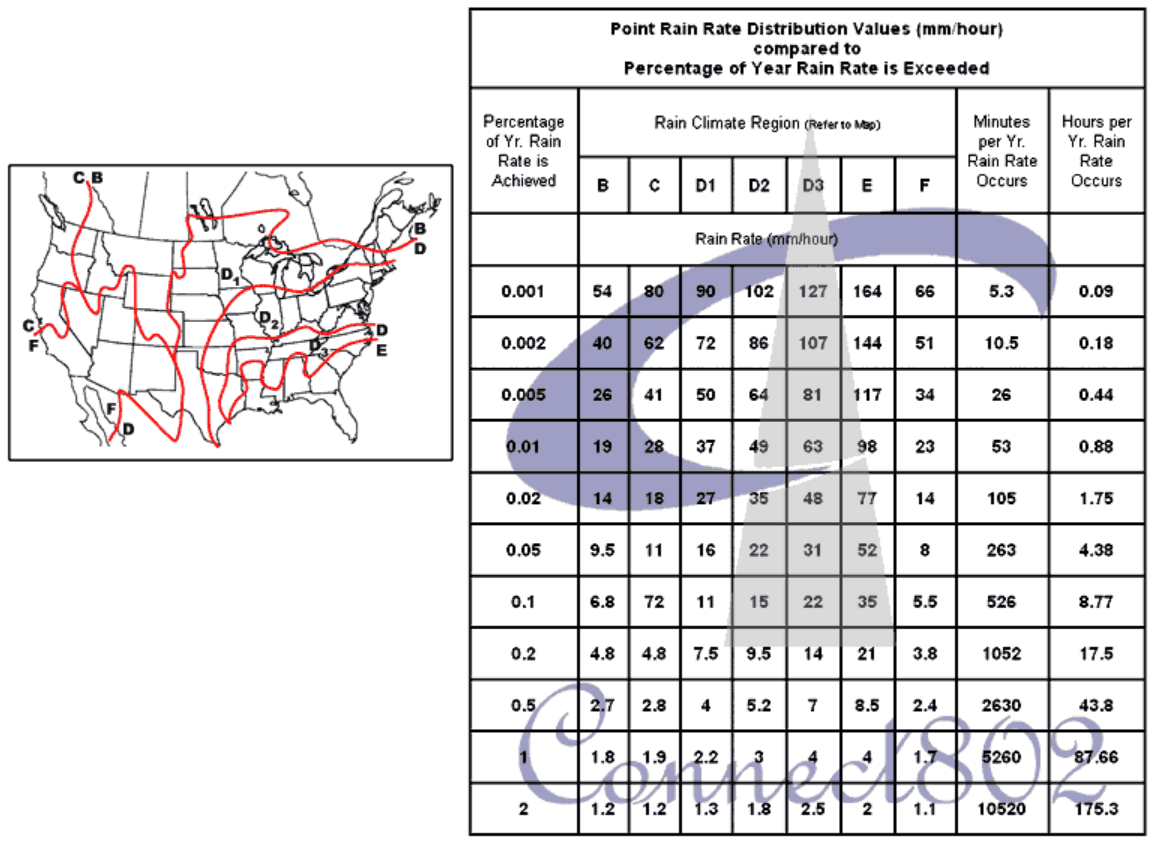
The Point Rain Rate Distribution table (above) let's you estimate, based on your Rain Region (from the map) how many hours/minutes per year your point-to-point link will be impacted by rain events. The Rain Fade Margin At Frequency graph (below) gives you an idea of how much attenuation will be introduced on the point-to-point link for a given rain rate (mm/hour) and Frequency (GHz).
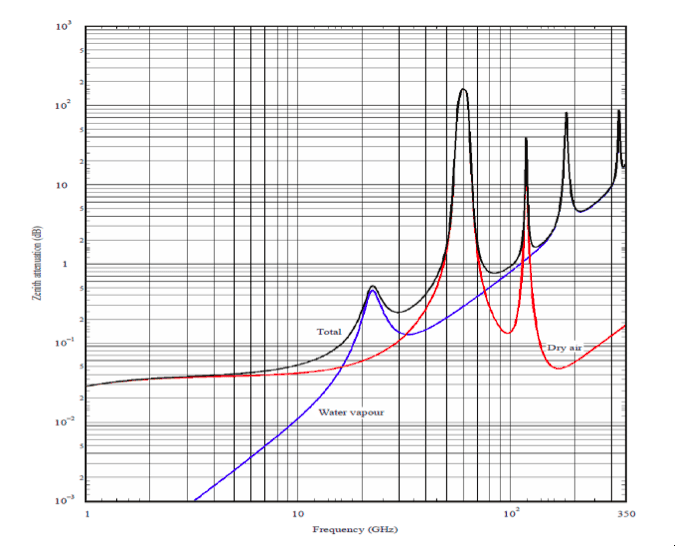
Background Atmospheric Attenuation
The Background Atmospheric Attenuation graph (above) shows the calculated total attenuation present in the normal, rain-free environment as a result of mid-range relative humidity (40% to 60%), "Water Vapour" blue line, plus the attenuation introduced by oxygen resonance in the air; the "Dry Air" red line.
Jump Back To Top Of Page
TERRAIN ROUGHNESS
Jump Back To Top Of Page
Value to Enter
Select the option that most accurately describes the terrain underneath the proposed radio link. The options are:
- Generally flat terrain surface
- Open parklands , farm land, water, airports (across the runway environment), thick jungle-like vegetation (where the link will pass over the consistent-height tree tops). Use Foliage Attenuation if the link must pass through trees
- Suburban area
- Buildings roughly the same height Housing developments, smaller town downtown area (generally rural communities), apartment complexes (when the link passes over the top of the complex), industrial parks (with similar-height warehouses and offices) ALSO gently rolling hills
- Urban area
- Buildings of different heights City downtown areas with many different building heights, large university campus environments (where the link passes over the campus) ALSO mountain areas with steep, undulating topography
- Ignore terrain roughness
- This option tells the calculator not to add any attenuation factor for terrain roughness
Significance of This Value
The Terrain Roughness selection describes the smoothness of the "top" of the span between the antennas. Some of this smooth (or irregular) "top" will penetrate the first 40% of the Fresnel Zone and, consequently, the degree to which it is smooth or rough will effect the degree to which the signal is reflected, diffracted, and attenuated. Remember that the height of the tallest obstruction will, ultimately, have to be added (by you, the designer; not by the calculator) to the antenna heights calculated by the Connect802 Antenna System Designer.
Background and Technical Perspective
An RF wave, propagating across a relatively smooth portion of the earth's surface (large lake, expansive meadow, etc.) will not "strike" the surface of the earth. By this it is meant that the curving surface always curves "away" or "down" while the wave continues to propagate in a direction that is essentially tangential to the sphere. This (when considered by itself) is the reason that the RF wavefront encounters less-dense atmosphere as it expands (the RF signal is moving tangentially to the sphere) which makes it refract downwards towards the earth resulting in the 4/3 factor for radio Line-of-Sight. (See discussion above under Tower Height).
When the earth's surface is not smooth, however, the RF signal will be absorbed, reflected, and diffracted to varying degrees by the terrain features that create "roughness". Very sophisticated RF modeling formulae exist that take into consideration specific terrain obstruction features. These formulae assess incident angles of RF rays as they refract and reflect from surfaces as well as using Gaussian distribution models of scattering losses. The Connect802 Antenna System Designer takes a more pragmatic approach to terrain roughness modeling. In "free space" (smooth surface) the assumption is made that an additional 2 dB of gain will be required to overcome the natural irregularities of the earth's surface. In suburban areas (where most buildings are the same height) a 3 dB gain is required, and in urban areas where there is dramatic height difference between buildings a 5 dB gain is added. Since exact sets of incident angle data are not typically available in most practical, field situations these values are appropriate. It's felt that this is a sufficiently reasonable approximation of what would otherwise be a calculation based on potentially unavailable input data.
LINK FADE MARGIN
Jump Back To Top Of Page
Value to Enter
Enter any additional fade margin you would like to apply to the calculation. A very widely used, "typical" link fade margin is 10 dB and this value becomes the default if no other value is entered. You may want to use a fade margin of 12 dB to be conservative and a fade margin of 6 dB to be aggressive. You could also considering Increasing your fade margin by and additional 3 dB in a highly reflective environment and by another 3 dB to 6 dB in an electrically noisy environment. Hence, a automotive repair shop, with many power tools and arc welding rigs might require a Link Fade Margin margin as high as 21 dB (12+3+6)
Significance of This Value
The Link Fade Margin is applied to link budget calculations as a way to compensate for normal and ordinary deviations in link characteristics. It comprises both "Fade Margin" (caused by multipath reflections) as well as other factors that may effectively attenuate the transmitted signal. There are a number of factors that may cause the theoretical calculations for a link to vary from the measured signal characteristics. The Link Fade Margin allows the designer to input additional loss that will be incorporated into calculated results.
Background and Technical Perspective
- Dynamic Environmental Conditions
- Theoretical RF engineering formulas use constants of proportionality that are based on average conditions and the real world has a dynamic range of condition measurements. Real-world conditions vary. Environmental conditions change from clear sky, to high humidity, to rain; and from hot to cold. Birds fly through elevated wireless links and people walk in the signal volume of ground-based antennas. The link fade margin is used as a "margin of error" to accommodate the practical expectations of a wireless link. It should be noted that Terrain Roughness can introduce additional fading, beyond any standard fade guidelines.
- Rayleigh Fading
- When signal energy leaves the transmitter it spreads out, forming a generally spherical wavefront. This wavefront propagates outwards and strikes various objects along its way. Some paths are generally straight from the transmitter to the receiver, others bounce off walls or objects and are longer. The difference in path lengths causes the composite signal to vary in strength. When the paths are of such a length as to cause received signals to arrive out of phase the signal strength goes down. This is called multipath fading, also called Rayleigh Fading. The design of a wireless system must consider Rayleigh Fading and must attempt to minimize the depth of any given fade event (the degree of signal reduction), the duration of the fade, and whether the fade causes the received signal to drop below the required receiver sensitivity. A system should be designed to operate at a low outage probability.
- Foliage Attenuation
- When trees are present, and the 60% radius of the 1st Fresnel Zone is penetrated by the tree line, the Link Fade Margin can be used to adjust for the foliage attenuation.
ANTENNA MAXIMUM LINEAR DIMENSION
Jump Back To Top Of Page
Value to Enter
Enter the length of the longest linear dimension of the antenna itself. For a dipole or yagi it's simply the length of the antenna. For a parabolic dish the dimension is the diameter of the dish. For any other shape, use the longest single dimension (which could be a diagonal across a rectangular element as in a grid sectional parabolic antenna.)
Significance of This Value
Near Field Radiation and the Near Field / Far Field Boundary distances are dependent on the value you enter for the Maximum Linear Dimension. These linear dimension value and the resulting calculated results do not change the dB gain/loss, antenna tower height, or suitability of the calculations. Therefore, if the dimension is left at its default "1 foot" value, or adjusted to your best estimation of size, it will not change the link-budget calculation. Knowing the Near Field/Far Field boundary will, however, give you insight into the installation location specifics for an antenna. For example:
When you enter a value for Max Linear Dimension, and check the corresponding radio button, the Connect802 Path Link Budget and Antenna Calculator uses that value, in conjunction with the transmission frequency, to calculate boundary between a region surrounding the antenna called the Near Field and the region further away, called the Far Field . This calculation, along with the calculation for the wavelength of the transmitted signal help to design a system that is not degraded by metal objects too close to the antenna.
Metal objects that are closer than the Near Field/Far Field Boundary distance relative to the radiating element of an antenna distort the transmission pattern. This distortion is used in a controlled way by antenna designers in Yagi and Grid antennas where reflecting and directing metal elements are positioned in a way that shapes the transmitted signal making the signal stronger in some directions than in others (a "directional antenna"). Don't mount antennas directly on solid metal objects (steel I-beams, light poles, etc.) or directly on a flat metal surface (aluminum siding or soffit material). In these cases, use a stand-off mount that positions the antenna at or beyond the Near Field/Far Field Boundary.
Metal objects in the Near Field region will significantly distort the antenna's transmit and receive characteristics. Metal objects that might accidentally end up in the Near Field or within 1/2 wavelength of the antenna include aluminum wall studs or plumbing pipe concealed behind drywall, ceiling supports in retail or warehouse buildings where the ceiling is exposed and an antenna is mounted on the support gridwork, and antenna towers where improper mounting places a side-mounted antenna too close to the tower. Keep metal objects a minimum of 1/2 wavelength away from any antenna and avoid metal objects in the Near Field as much as is practical.
Background and Technical Perspective
The electric current impressed on the radiating element of an antenna alternates in strength at the frequency of the transmitter (2.4 GHz, 5.8Hz, etc.) During the first 1/4 of each wavelength the current is increasing, creating an expanding magnetic field around the conductor. During the next 1/4 cycle the current is decreasing to zero, and the magnetic field collapses. A portion of the energy stored in the magnetic field is returned to the radiating element. This is called the induction energy. It is the energy stored in the magnetic field during one 1/4 cycle, and returned to the antenna in the next. Induction energy exists only in very close proximity to the radiating element. This region is called the Near Field. Induction energy is greatest within 1/2 wavelength of the radiating element.
The expanding and collapsing magnetic field sets in motion an electromagnetic field that continues to expand away from the antenna. This is called the radiating energy and this is what travels through space between the transmitter and receiver. It's the radiating energy that we normally think about when considering a wireless network design. Radiating energy exists in the region called the Far Field. The Far Field is also referred to as the Fraunhofer Region after Joseph Fraunhofer who is best known for his work in the early 1800's with spectral absorption lines, the dark lines in a solar spectrum that help scientists determine the chemical makeup of stars.
Because the radiating characteristics of an antenna are closely related to the interaction of the collapsing Near Field and the radiating element it can be useful to know the distance to the boundary between the Near Field and the Far Field. A metal object in the Near Field will absorb some of the induction energy created by the antenna. Since there is no transmitter circuitry attached to this metal object there is no place for the induced energy to go. The energy is re-radiated from the metal object just as if the object were another antenna. When these interactions are carefully calculated the elements of a Yagi antenna can be designed so as to create a directional beam. When the interactions are the result of unintended metal objects in the environment they can cause unexpected antenna behaviors.
A detailed discussion of the Near Field and Far Field must take place in a context that is well outside the scope of the present overview. Keep unintended metal objects out of the Near Field as much as is practical and definitely avoid metal objects within 1/2 wavelength of the radiating element.
Connect802 Disclaimer
Do not depend solely on the results calculated by the Connect802 Antenna System Designer in any case were loss of life, property damage, or other liability is at risk relative to the proposed point-to-point wireless link being designed. Results may be subject to arithmetic rounding errors. This calculator is designed to provide results with a level of precision that is sufficient for use in typical outdoor, point-to-point wireless network design. Calculated values represent the arbitrary arithmetic results of standard path loss, Fresnel zone, earth curvature, and link budget formulas. Measurements made in the field may vary from those calculated here since manufacturing tolerances and measurement accuracy introduce variability. Attenuation in cable connectors may vary substantially from theoretical values if oxidation is present. While every effort has been made to assure the accuracy of the calculations, Connect802 makes no guarantee of the accuracy or suitability of this information. Contact Connect802 with any questions or concerns. "We've Got You Covered!"

